1. Властивості середньої лінії трапеції
2. Доказ теореми про середньої лінії трапеції

Середня лінія трапеції, а особливо її властивості, дуже часто використовуються в геометрії для вирішення завдань і докази тих чи інших теорем.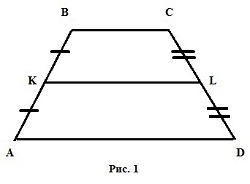

Трапеція - це чотирикутник, у якого тільки 2 сторони паралельні один одному. Паралельні сторони називають підставами (на малюнку 1 - AD і BC), дві інші - бічними (на малюнку AB і CD).

Середня лінія трапеції - це відрізок, що з'єднує середини її бічних сторін (на малюнку 1 - KL).

Властивості середньої лінії трапеції

1. Довжина середньої лінії дорівнює половині суми довжин її підстав:

   

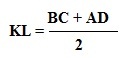
2. Середня лінія завжди паралельна її підстав.

Доказ теореми про середньої лінії трапеції

Довести, що середня лінія трапеції дорівнює напівсумі її підстав і паралельна цих підстав.

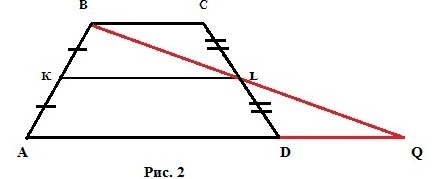
Дана трапеція ABCD із середньою лінією KL. Для доказу розглянутих властивостей потрібно провести пряму через точки B і L. На малюнку 2 це пряма BQ. А також продовжити підставу AD до перетину з прямою BQ.

Розглянемо отримані трикутники LBC і LQD:

1. За визначенням середньої лінії KL точка L є серединою відрізка CD. Звідси випливає, що відрізки CL і LD рівні.
2. ∠ BLC = ∠ QLD, так як ці кути вертикальні.
3. ∠ BCL = ∠ LDQ, так як ці кути навхрест лежачі при паралельних прямих AD і BC і січною CD.

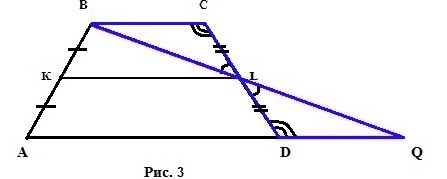
З цих 3 рівностей випливає, що розглянуті раніше трикутники LBC і LQD рівні по 1 стороні і двом прилеглим до неї кутам (див. Рис. 3). Отже, ∠ LBC = ∠ LQD, BC = DQ і найголовніше - BL = LQ => KL, що є середньою лінією трапеції ABCD, також є і середньою лінією трикутника ABQ. Відповідно до властивості середньою лінією трикутника ABQ отримуємо:

1. KL = 1 / 2AQ = 1/2 (AD + DQ) = 1/2 (AD + BC)
2. KL || AD по властивості середньої лінії трикутника. А так як AD || BC за визначенням трапеції, то KL || BC.

Для закріплення матеріалу рекомендуємо Вам переглянути відео урок з даної теми:

Швидше за все, Вам буде цікаво: